跳转至

PQ 樹

PQ 樹是一種基於樹的數據結構，代表一組元素上的一系列排列，由 Kellogg S. Booth 和 George S. Lueker 於 1976 年發現命名，用來解決以下問題

給出 \(m\) 個集合 \(S_i\)，你要找到一個 \(1\sim n\) 的排列，使得每個集合內的元素都相鄰。

PQ 樹可以在 \(O(n+\sum|S_i|)\) 時間內構建。本文中介紹的構建方法時間複雜度為 \(O(nm)\)。

定義

PQ 樹有三種結點：葉子結點、P 結點 和 Q 結點。其中葉子結點代表排列中的一個元素，P 結點表示它的子結點可以任意排列，Q 結點表示它的兒子順序可以反轉。所有非葉子結點都是 P 結點或 Q 結點中的一種。P 結點至少有 2 個兒子，Q 結點至少有 3 個兒子。
由於結點的定義，PQ 樹本身代表了 所有的 合法方案，其先序遍歷就是其中之一。
下圖是一棵 PQ 樹。

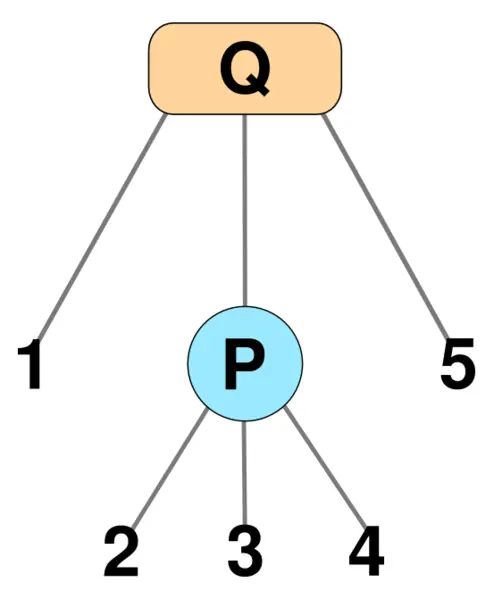
其先序遍歷 1,2,3,4,5 代表了一個合法方案。如果 P 結點的兒子重排列為 4,2,3，我們得到了另一個合法方案 1,4,2,3,5。保持 P 結點兒子順序不變，Q 結點的兒子順序反轉，得到了另一個合法方案 5,3,2,4,1。

構建

PQ 樹使用兒子 - 兄弟表示法。

我們增量構建一棵 PQ 樹。

首先建立一棵樹，其根為 P，總共 \(n\) 個兒子，分別是 \(1,2,\ldots,n\)，代表沒有任何限制時的 PQ 樹。隨着限制的不斷加入，我們不斷修改這棵樹。

當加入一個新的限制集合 \(S\) 時，我們把所有屬於這個集合的葉子結點標記為 黑色，不在這個集合內的葉子結點標記為 白色。對於所有非葉子結點，如果其所有兒子均為黑色，將其也標記為黑色；如果其所有兒子均為白色，將其也標記為白色；否則將其標記為 灰色。在下面的圖中，黑色結點、白色結點、灰色結點分別用黑色、灰色、一半黑一半灰來表示。

我們要求 PQ 樹中的結點按照顏色排序。

自底向上法

包含所有黑色結點的最小子樹被稱為 相關子樹，相關子樹的根（不一定是整棵樹的根）被稱為 相關根。

添加一個限制的過程被稱為 reduction。一次 reduction 分為兩個階段：冒泡階段和減少階段。

冒泡階段

冒泡階段只處理相關子樹。我們將相關子樹中的所有結點標記為黑色或灰色，併為每個結點計算其擁有的相關子結點數量。為了高效地完成這個過程，我們從葉子往根處理相關子樹。這需要記錄每個點的父親結點，但在減少階段一個點的父親結點經常要被修改。為了在線性時間內構造，只有 P 結點的兒子和 Q 結點的最後一個兒子 始終記錄正確的父親結點。對於 Q 結點的其他兒子，在冒泡階段用最後一個兒子的父親更新他們的父親。

當遇到一箇中間的結點時，我們看一下它的兄弟是否已經有合法的父親結點。如果沒有，將其標記為 阻塞 的。如果後面它的兄弟有了合法的父親，那麼修改這個結點的父親並且取消標記。如果在冒泡階段結束時，仍然有一段連續的阻塞結點（如下面的情況 Q3），一個沒有父結點的「偽結點」成為該塊的父結點，並在減少階段時被去除。

減少階段

減少階段用一個隊列來處理結點。首先將所有限制內的葉子結點加入隊列。每次取出隊首的結點 \(u\) 並處理。如果 \(u\) 的父親也是相關子樹內的結點，那麼將 \(\mathit{fa}_u\) 入隊。
對於每一個結點 \(u\)，我們分情況討論。如果不屬於其中任何一種情況，則無解。

葉子結點

將 \(u\) 標記為黑色。

P 結點

如果所有兒子均為黑色，將 \(u\) 標記為黑色。

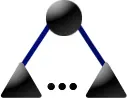
如果 \(u\) 有黑色兒子和白色兒子，且 \(u\) 是相關根，那麼新建一個 P 結點 \(v\) 成為它所有黑色兒子的根。

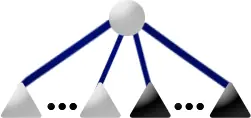
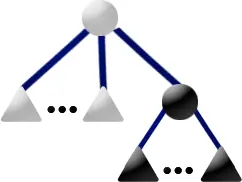
如果 \(u\) 有黑色兒子和白色兒子，且 \(u\) 不是相關根，那麼做以下操作：

  • 新建一個 P 結點 \(f\) 成為所有黑色兒子的根。
  • 新建一個 P 結點 \(e\) 成為所有白色兒子的根。
  • 如果 \(e\)（和/或 \(f\)）只有一個兒子，那麼不要新建結點，而是將 \(e\)（和/或 \(f\)）直接賦值成那個兒子。
  • 將 \(u\) 改成 Q 結點並把其兒子設為 \(e\) 和 \(f\)，將其標記為灰色。

注意到根據之前的定義，Q 結點至少有 3 個兒子，因此這裏的 \(u\) 被視為一個「偽結點」，並且將在後面被繼續處理。

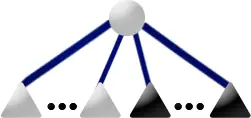
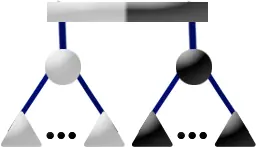
如果 \(u\) 有一個灰色兒子 \(p\)，且 \(u\) 是相關根，那麼新建一個 P 結點 \(v\) 作為其所有黑色兒子的根，將 \(v\) 的兄弟設為 \(p\) 最後一個一個黑色兒子，然後把 \(v\) 設為 \(p\) 的最後一個兒子。

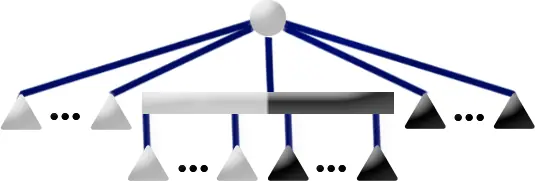
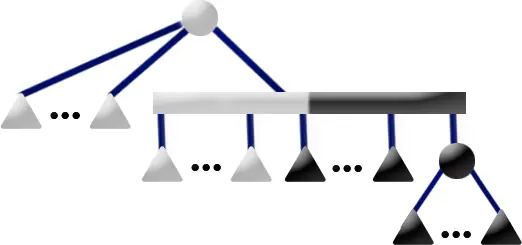
如果 \(u\) 有一個灰色兒子 \(p\)，且 \(u\) 不是相關根，那麼進行以下操作：

  • 新建一個 P 結點 \(f\) 成為所有黑色兒子的根。
  • 新建一個 P 結點 \(e\) 成為所有白色兒子的根。
  • 如果 \(e\)（和/或 \(f\)）只有一個兒子，那麼不要新建結點，而是將 \(e\)（和/或 \(f\)）直接賦值成那個兒子。
  • 將 \(e\) 的兄弟設為 \(p\) 最後一個白色兒子，然後把 \(e\) 設為 \(p\) 的最後一個兒子。
  • 將 \(f\) 的兄弟設為 \(p\) 最後一個黑色兒子，然後把 \(f\) 設為 \(p\) 的最後一個兒子。


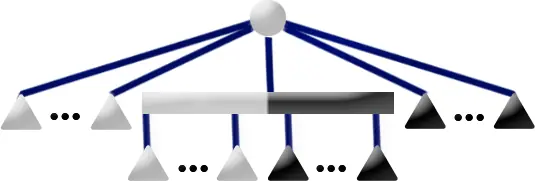
如果 \(u\) 恰有兩個灰色兒子 \(p_1,p_2\)，那麼進行以下操作：

  • 新建一個 P 結點 \(f\) 成為所有黑色兒子的根。
  • 如果 \(f\) 只有一個兒子，那麼不要新建結點，而是將 \(f\) 直接賦值成那個兒子。
  • 把 \(p_1\) 的最後一個黑色兒子的兄弟設為 \(f\)。
  • 把 \(f\) 的兄弟設為 \(p_2\) 的最後一個黑色兒子。
  • 把 \(p_2\) 的最後一個兒子設為 \(p_2\) 的最後一個白色兒子。

可以發現這樣 \(p_2\) 就被合併進了 \(p_1\)。

Q 結點

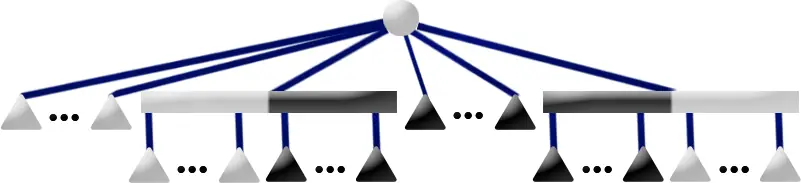
如果 \(u\) 只有黑色兒子，那麼將 \(u\) 標記成黑色。（下面的圖的形狀錯了。）

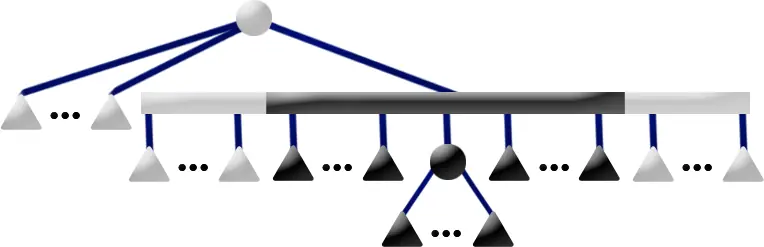
如果 \(u\) 有一個灰色兒子 \(p\)，且所有標記相同的兒子均連續出現，那麼進行如下操作：

  • 設 \(p_f\) 為 \(p\) 最後一個黑色兒子，\(p_e\) 為 \(p\) 最後一個白色兒子，\(f\) 為 \(p\) 的黑色兄弟，\(e\) 為 \(p\) 的白色兄弟。
  • 將 \(f\) 的兄弟設為 \(p_f\)，\(e\) 的兄弟設為 \(p_e\)。
  • 如果 \(p\) 沒有一個白色兄弟或黑色兄弟，將 \(u\) 的最後一個兒子設成 \(p\) 的最後一個兒子。
  • 刪除 \(p\)。


如果 \(u\) 恰有兩個灰色兒子 \(p_1,p_2\)，且所有標記相同的兒子均連續出現，那麼對 \(p_1,p_2\) 都進行上一種操作即可。

該構建方法是原論文中的，但是實現較為不便。

自頂向下法

目前 OI 中的實現大多采用該方法。其實方法類似，下面出現的情況基本都能在上面找到。

注意到根據之前的染色過程，所有黑色和白色的點都已經滿足條件，因此我們 只需要處理灰色結點。

P 結點

  • 如果 \(u\) 有多於兩個灰色兒子，無解。
  • 如果 \(u\) 只有一個灰色兒子，且沒有黑色兒子，遞歸處理灰色兒子。
  • 否則先清空 \(u\) 的兒子，然後加入所有的白色兒子。新建一個 Q 結點 \(q_1\) 併成為 \(u\) 的兒子。在 \(q_1\) 中加入所有的灰色兒子。新建一個 P 結點 \(p\) 作為所有黑色兒子的根，將 \(p\) 插入 \(q_1\) 的中間。（對應了自底向上法 P 結點的所有情況。）

注意到我們會要求兩個灰色節點白色全在左側，黑色全在右側（或相反），因此我們需要實現一個分裂函數 split，可以把這個子樹的點分裂成黑白部分，並同時保留分裂成的子樹的節點的 所有可能。

Q 結點

  • 找到最左邊和最右邊的非白色節點位置 \(l,r\)。如果 \([l+1,r-1]\) 內有非黑色節點，無解。
  • 如果沒有黑色節點，只有一個灰色節點，遞歸處理這個灰色節點，否則只需要將 \(l\) 和 \(r\) 位置的節點分裂。

分裂函數

令要分裂的點為 \(u\)，我們想把 \(u\) 分裂成左邊全是白色，右邊全是黑色的森林。如果 \(u\) 不是灰色結點則直接返回子樹。只考慮灰色結點的情況。 如果 \(u\) 是 P 類結點：

  • 如果 \(u\) 有至少兩個灰色兒子，則無解。
  • 否則左邊是所有白色兒子，中間遞歸處理灰色兒子，右邊是所有黑色兒子。注意到要保留所有的可能，因此要新建兩個 P 結點分別作為白色兒子和黑色兒子的根。（對應自底向上法的 P4 情況。）
  • 刪除 \(u\)。

如果 \(u\) 是 Q 類結點：

  • 如果正序和反序都不滿足白 - 灰 - 黑，則無解。
  • 如果有至少兩個灰色兒子，也無解。
  • 否則遞歸分裂灰色兒子即可。
  • 刪除 \(u\)。

最後把所有多餘的結點（只有一個兒子的結點）刪除。

代碼實現

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
class PQTree {
 public:
  PQTree() {}

  void Init(int n) {
    n_ = n, rt_ = tot_ = n + 1;
    for (int i = 1; i <= n; i++) g_[rt_].emplace_back(i);
  }

  void Insert(const std::string &s) {
    s_ = s;
    Dfs0(rt_);
    Work(rt_);
    while (g_[rt_].size() == 1) rt_ = g_[rt_][0];
    Remove(rt_);
  }

  std::vector<int> ans() {
    DfsAns(rt_);
    return ans_;
  }

  ~PQTree() {}

 private:
  int n_, rt_, tot_, pool_[100001], top_, typ_[100001] /* 0-P 1-Q */,
      col_[100001] /* 0-black 1-white 2-grey */;
  std::vector<int> g_[100001], ans_;
  std::string s_;

  void Fail() {
    std::cout << "NO\n";
    std::exit(0);
  }

  int NewNode(int ty) {
    int x = top_ ? pool_[top_--] : ++tot_;
    typ_[x] = ty;
    return x;
  }

  void Delete(int u) { g_[u].clear(), pool_[++top_] = u; }

  void Dfs0(int u) {  // get color of each node
    if (u >= 1 && u <= n_) {
      col_[u] = s_[u] == '1';
      return;
    }
    bool c0 = false, c1 = false;
    for (auto &&v : g_[u]) {
      Dfs0(v);
      if (col_[v]) c1 = true;
      if (col_[v] != 1) c0 = true;
    }
    if (c0 && !c1)
      col_[u] = 0;
    else if (!c0 && c1)
      col_[u] = 1;
    else
      col_[u] = 2;
  }

  bool Check(const std::vector<int> &v) {
    int p2 = -1;
    for (int i = 0; i < static_cast<int>(v.size()); i++)
      if (col_[v[i]] == 2) {
        if (p2 != -1) return false;
        p2 = i;
      }
    if (p2 == -1)
      for (int i = 0; i < static_cast<int>(v.size()); i++)
        if (col_[v[i]]) {
          p2 = i;
          break;
        }
    for (int i = 0; i < p2; i++)
      if (col_[v[i]]) return false;
    for (int i = p2 + 1; i < static_cast<int>(v.size()); i++)
      if (col_[v[i]] != 1) return false;
    return true;
  }

  std::vector<int> Split(int u) {
    if (col_[u] != 2) return {u};
    std::vector<int> ng;
    if (typ_[u]) {  // Q
      if (!Check(g_[u])) {
        std::reverse(g_[u].begin(), g_[u].end());
        if (!Check(g_[u])) Fail();
      }
      for (auto &&v : g_[u])
        if (col_[v] != 2) {
          ng.emplace_back(v);
        } else {
          auto s = Split(v);
          ng.insert(ng.end(), s.begin(), s.end());
        }
    } else {  // P
      std::vector<int> son[3];
      for (auto &&x : g_[u]) son[col_[x]].emplace_back(x);
      if (son[2].size() > 1) Fail();
      if (!son[0].empty()) {
        int n0 = NewNode(0);
        g_[n0] = son[0];
        ng.emplace_back(n0);
      }
      if (!son[2].empty()) {
        auto s = Split(son[2][0]);
        ng.insert(ng.end(), s.begin(), s.end());
      }
      if (!son[1].empty()) {
        int n1 = NewNode(0);
        g_[n1] = son[1];
        ng.emplace_back(n1);
      }
    }
    Delete(u);
    return ng;
  }

  void Work(int u) {
    if (col_[u] != 2) return;
    if (typ_[u]) {  // Q
      int l = 1e9, r = -1e9;
      for (int i = 0; i < static_cast<int>(g_[u].size()); i++)
        if (col_[g_[u][i]]) checkmin(l, i), checkmax(r, i);
      for (int i = l + 1; i < r; i++)
        if (col_[g_[u][i]] != 1) Fail();
      if (l == r && col_[g_[u][l]] == 2) {
        Work(g_[u][l]);
        return;
      }
      std::vector<int> ng;
      for (int i = 0; i < l; i++) ng.emplace_back(g_[u][i]);
      auto s = Split(g_[u][l]);
      ng.insert(ng.end(), s.begin(), s.end());
      for (int i = l + 1; i < r; i++) ng.emplace_back(g_[u][i]);
      if (l != r) {
        s = Split(g_[u][r]);
        std::reverse(s.begin(), s.end());
        ng.insert(ng.end(), s.begin(), s.end());
      }
      for (int i = r + 1; i < static_cast<int>(g_[u].size()); i++)
        ng.emplace_back(g_[u][i]);
      g_[u] = ng;
    } else {  // P
      std::vector<int> son[3];
      for (auto &&x : g_[u]) son[col_[x]].emplace_back(x);
      if (son[1].empty() && son[2].size() == 1) {
        Work(son[2][0]);
        return;
      }
      g_[u].clear();
      if (son[2].size() > 2) Fail();
      g_[u] = son[0];
      int n1 = NewNode(1);
      g_[u].emplace_back(n1);
      if (son[2].size() >= 1) {
        auto s = Split(son[2][0]);
        g_[n1].insert(g_[n1].end(), s.begin(), s.end());
      }
      if (son[1].size()) {
        int n2 = NewNode(0);
        g_[n1].emplace_back(n2);
        g_[n2] = son[1];
      }
      if (son[2].size() >= 2) {
        auto s = Split(son[2][1]);
        std::reverse(s.begin(), s.end());
        g_[n1].insert(g_[n1].end(), s.begin(), s.end());
      }
    }
  }

  void Remove(int u) {  // remove the nodes with only one child
    for (auto &&v : g_[u]) {
      int tv = v;
      while (g_[tv].size() == 1) {
        int t = tv;
        tv = g_[tv][0];
        Delete(t);
      }
      v = tv, Remove(v);
    }
  }

  void DfsAns(int u) {
    if (u >= 1 && u <= n_) {
      ans_.emplace_back(u);
      return;
    }
    for (auto &&v : g_[u]) DfsAns(v);
  }
} T;

習題

參考資料

本页面最近更新：，更新历史
发现错误？想一起完善？ 在 GitHub 上编辑此页！
本页面贡献者：isdanni,xyf007
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供，附加条款亦可能应用